栈（Stack）和队列（Queue），了解栈和队列的基础知识，学习它们的基础应用。

栈 Stack

栈 Stack 是一种线性结构，是线性表的一种具体形式。栈这种后进先出（Last In First Out，LIFO）的应用非常广泛，例如网页的前进后退功能，编辑器的后一步前一步功能，方法调用时的函数栈等等。

栈 Stack 的特性：

• 栈的元素必须“后进先出”
• 栈的操作只能于线性表表尾进行
• 栈的表尾被称为栈顶（Top），栈的表头被称为栈底（bottom）

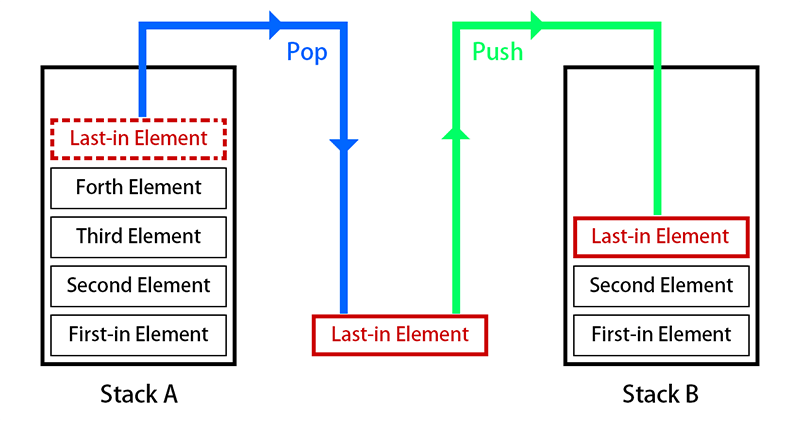
栈 Stack 的操作：

• 插入操作（Push），进栈
• 删除操作（Pop），出栈

栈的顺序存储结构

应用顺序存储结构的栈，元素必须从开始表尾进行操作，从而节省下元素前移补充位置的操作，而不像链式结构可以从表头操作。当栈初始化时，不含有任何数据的栈被称为空栈，此时栈顶就是栈底。

栈的链式存储结构

栈一般使用顺序存储结构 实现。使用链式存储结构时，栈底为链表头部，栈顶为链表尾部。

使用栈来进行进制转换

例子，使用顺序存储结构的栈计算把 8 位数的二进制数转换成十进制数。

let stack = [1, 1, 0, 0, 1, 0, 0, 1]; // 11001001 (2)
// 1*2^0 + 0*2^1 + 0*2^2 + 1*2^3 + 0*2^4 + 0*2^5 + 1*2^6 + 1*2^7
let result = 0;
let power = 0; // start with power of 0 in first digit
while (stack.length) {
  result += stack.pop() * Math.pow(2, power++);
}
// result = 201 (10)

// Faster way in JavaScript
parseInt('11001001', 2).toString(10);

例子，使用顺序存储结构的栈计算把 8 位数的二进制数转换成八进制数。

let stack = [1, 1, 0, 0, 1, 0, 0, 1]; // 11001001 (2)
// 001=>1, 001=>1, 11=>3, final 311 (8)
let temp = [];
while (stack.length) {
  // 3-digit pair
  let d0 = stack.pop() | 0;
  let d1 = (stack.pop() | 0) * 2;
  let d2 = (stack.pop() | 0) * 4;
  let D = d0 + d1 + d2;
  temp.push(D);
}
let result = temp.reverse().join(''); // result = 311 (8)
temp = parseInt(result, 8); // 201 (10)

// Faster way in JavaScript
parseInt('11001001', 2).toString(8);

例子，使用顺序存储结构的栈计算把 8 位数的二进制数转换成十六进制数。

let stack = [1, 1, 0, 0, 1, 0, 0, 1]; // 11001001 (2)
// 1001=>9, 1100=>C, final C9 (16)
let letters = ['a', 'b', 'c', 'd', 'e', 'f'];
let temp = [];
while (stack.length) {
  // 4-digit pair
  let d0 = stack.pop() | 0;
  let d1 = (stack.pop() | 0) * 2;
  let d2 = (stack.pop() | 0) * 4;
  let d3 = (stack.pop() | 0) * 8;
  let D = d0 + d1 + d2 + d3;
  temp.push(D > 9 ? letters[D % 10] : D);
}
let result = temp.reverse().join(''); // result = C9 (16)
temp = parseInt(result, 16); // 201 (10)

// Faster way in JavaScript
parseInt('11001001', 2).toString(16);

使用栈来计算普通数学表达式

计算1 + (2 - 3 * 4.5) / 6;

第一步，转换中缀表达式到后缀表达式（逆波兰表达式）。

// Expected Result: 1 2 3 4.5 * - 6 / +
let input = '1 + (2 - 3 * 4.5) / 6';
input = input.replace(/\s/g, ''); // 1+(2-3*4.5)/6
let numbers = input.split(/[\+\-\*\/\(\)]+/);
// ["1", "2", "3", "4.5", "6"]
numbers.forEach((num, i) => {
  input = input.replace(num, i); // 0+(1-2*3)/4
});
let result = '';
let stack = [];
for(let i = 0; i < input.length; i++) {
  let value = input.charAt(i);
  if (/[\+\-\*\/\(\)]/.test(value)) {
    if (value === ')') {
      let symbol = stack.pop();
      while (symbol !== '(') {
        result += `${symbol} `;
        symbol = stack.pop();
      }
    } else {
      if (stack.length > 0) {
        let symbol = stack.pop();
        if (/\*\//.test(symbol) && !/\*\//.test(value)) {
          result += `${symbol} `;
        } else {
          stack.push(symbol);
        }
      }
      stack.push(value);
    }
  } else {
    result += `${numbers[value]} `;
  }
}
while (stack.length > 0) {
  result += `${stack.pop()} `;
}

// result = "1 2 3 4.5 * - 6 / +"

第二步，计算转换后的逆波兰表达式，最后输出结果。

// Expected Result: -0.9166666666666667
let input = '1 2 3 4.5 * - 6 / +';
input = input.trim().split(/\s/);
// ["1", "2", "3", "4.5", "*", "-", "6", "/", "+"]
let stack = [];
let result = 0;
for (let i = 0; i < input.length; i++) {
  let value = input[i];
  if (isNaN(value)) {
    let backNum = stack.pop();
    let frontNum = stack.pop();
    let subResult = 0;
    if (value === '+') {
      subResult = frontNum + backNum;
    } else if (value === '-') {
      subResult = frontNum - backNum;
    } else if (value === '*') {
      subResult = frontNum * backNum;
    } else if (value === '/') {
      if (backNum === 0) {
        throw new Error('Divisor cannot be 0');
      }
      subResult = frontNum / backNum;
    } else {
      throw new Error('Operator must be"+","-","*"or"/"');
    }
    if (stack.length > 0) {
      stack.push(subResult);
    } else {
      result = subResult;
    }
  } else {
    stack.push(parseFloat(value));
  }
}

// result = -0.9166666666666667

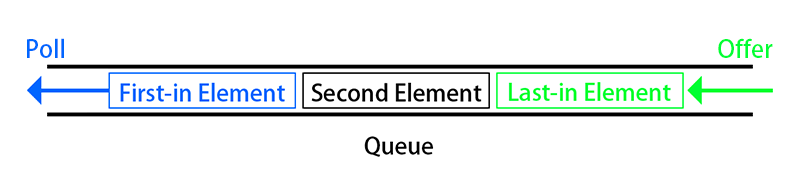
队列 Queue

队列 Queue 是一种线性结构，也是线性表的一种具体形式。队列这种先进先出（First In First Out，FIFO）的应用也非常广泛，是只允许在一段进行插入操作，而在另一端进行删除操作的线性表，例如输入缓冲功能，任务顺序加载功能等等。

队列可以用顺序储存结构实现，但是跟栈相反，队列一般都用链式储存结构 实现。

队列 Queue 的特性：

• 队列的元素必须“后进先出”
• 队列的操作只能于线性表头尾进行

队列 Queue 的操作：

• 插入操作（Offer），进队列
• 删除操作（Poll），出队列

本文参考：
【C 语言描述】《数据结构和算法》（小甲鱼） (opens new window)