线性表（List），了解线性表的基础知识，认识一下线性表的种类。

线性表 List

线性表（List）：由另个或多个元素组成的有限序列。元素是有序的，可以被排列的 。在有序结构中，某个元素ai 前面的元素 ai-1 称为 前驱元素 ，后面的元素ai+1 称为 后继元素。在 Java 语言中，数组（ArrayList）和链表（Linked List）都属于线性表。其中数组使用了顺序结构，而链表使用了链式结构。

线性表的数据对象集合为 {a1,a2,...,an-1,an}，每个元素的类型均为DataType。** 数据元素之间的关系是一对一的关系。** 其中，除第一个元素a1 外，每个元素有且只有一个直接前驱元素，除最后一个元素 an 外，每个元素有且只有一个直接后继元素。

线性表伪代码

ADT 线性表（List）
Data
  数据对象集合 {a1,a2,...,an-1,an}
Operation
  init(*L)：初始化空线性表 L
  isEmpty(L)：判断线性表是否为空
  clear(*L)：清空线性表
  getElement(L,i,*e)：将线性表 L 中第 i 个元素返回给 e
  elementAt(L,e)：线性表 L 中查找与 e 相等的元素，返回元素的位置
  insert(*L,i,e)：线性表 L 中第 i 个位置插入新元素 e
  delete(*L,i,*e)：删除线性表 L 中第 i 个位置元素，并返回该元素给 e
  length(L)：返回线性表 L 的元数个数
endADT

1
2
3
4
5
6
7
8
9
10
11
12
13

线性表的顺序存储结构

线性表的顺序存储结构封装需要 3 个属性：

存储空间初始位置，数组指针
线性表的最大长度，指存储空间总长度，初始化后不变
线性表的当前长度，指表中元素数量，大于等于 0，小于表的最大长度

顺序存储结构的地址计算方法

注：i从“1”开始

假设每个元素类型的 DataType 都需要占用 c 个储存单位（字节），那么线性表中第 i+1 个元素和第 i 个元素的存储位置的关系是（LOC 为获得存储位置的函数）：

LOC(ai+1) = LOC(ai) + c

所以找第 i 个元素 ai 的储存位置可以又线性表初始指针指向的 a1 推算出：

LOC(ai) = LOC(a1) + (i-1) * c

通过这个公式，计算出线性表中任意位置的地址，所用的时间都是相同的，那么他的存储时间性能就是 O(1)， 这种结构通常被称为随机存储结构。

线性表的链式存储结构

顺序存储结构最大的缺点，插入和删除需要移动大量元素，从而保持表中元素邻居的关系；链式存储结构通过携带后继元素的存储地址就解决了这个缺点。

链式存储结构的线性表中元素称为“存储映像”，也称为“节点（Node）”。每个节点都是由两部分组成：

数据域：储存数据元素信息的域
指针域：存储直接后继元素地址的域

单链表

n个节点链接成一个链表，即为线性表 (a1,a2,...,an-1,an) 的链式存储结构。因为此链表的每个节点中只包含一个指针域，所以叫做单链表。

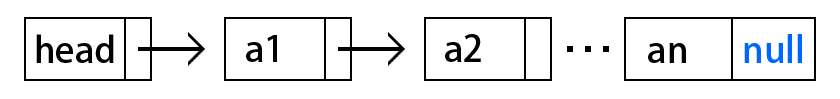
单链表图示

单链表必须有一个头部加上 0 到多个节点。头指针是链表指向第一个节点的指针，如果链表有头结点，则头指针指向头结点。头结点携带第一个元素的节点指针，放在第一个节点之前，其数据域一般无意义，但也可以存放链表的长度。头结点不是必须的，但是头结点可以放一些对列表有用的变量。

尾指针是指向单链表的最后一个节点的指针，这个指针不是必须的，但是尾指针有好处，比如需要在尾部插入新节点。

若线性表需要频繁查找，很少进行插入和删除操作是，宜采用顺序存储结构。

若需要频繁插入和删除时，宜采用单链表结构。

静态链表

在内存中建立一个数组，在数组最大长度内的空间中再建立一个链表，这种链表就是静态链表。静态链表通过“游标（Cursor）”指向后继元素所处数组中的“下标（Index）”。下图为静态链表转普通链表，最大长度为100，第一个元素游标指向备用链表的头节点（既当前链表尾节点的游标，也是尾指针），最后一个元素游标指向当前链表头节点。

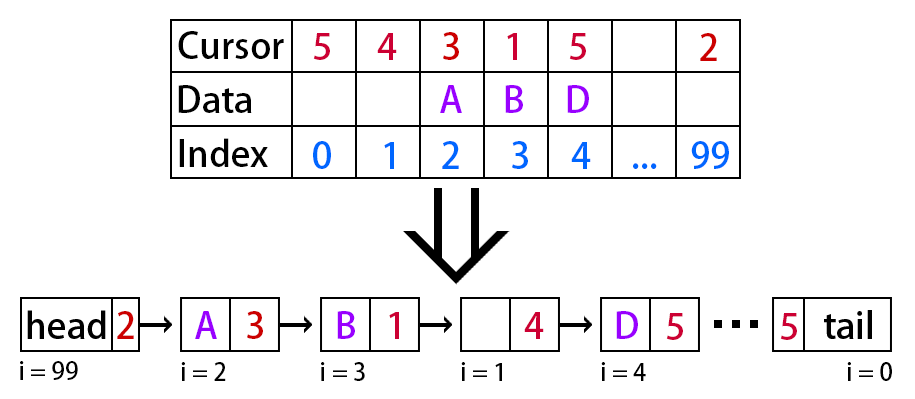
静态链表转普通链表

数组中第一个和最后一个元素不存放数据
未使用的数组元素被称为备用链表
数组第一个元素，即 Index = 0 的元素的游标（Cursor）存放备用链表的第一个节点的下标
数组最后一个元素，即 Index = MAX_SIZE-1 的元素的游标（Cursor）存放当前链表的第一个节点的下标
静态链表初始化时，Index = 0的元素的游标应从 1 开始，而 Index = MAX_SIZE-1 的元素的游标则是0，表示空链表

循环链表

在单链表中，如果不从头结点出发，就无法访问到全部节点。循环链表就解决了这个问题。只要有链表中某一节点的指针，就能跑完全部节点。当表为空时，头部后继指针指向头部本身。

循环链表所用的方法就是把尾节点的空指针指向头节点，使单链表形成一个环，这种头尾相接的单链表被称为单循环链表，简称循环链表。

原单链表判断尾节点用node.next === null ?，现在则是用node.next === head ?。

双向链表

对比单链表，双向链表的节点有两个指针：前驱指针和后继指针。双向列表允许从尾部往回跑。当表为空时，头部前驱指针和后继指针都指向头部本身。

找单链表中间的节点的方法

利用快慢指针原理：设置两个指针 *search 和*middle都指向单链表的头结点。其中 *search 的移动速度是 *middle 的 2 倍。当 *search 指向尾节点时，*middle正好就在中间。

在一个长度为 100 的单链表中，当 *search 指向第 100 个节点时，*middle指向第 50 个节点。

在一个长度为 101 的单链表中，当 *search 指向 102（即超出长度）时，*middle指向第 51 个节点，正好在中间。

判断一个链表是否有环

方法一：设置两个指针 *q 和*b。*q一直在走的情况下，每遇到一个节点，*b就从新从头结点开始走。如果 *q 所在当前步数等于 *b 从头开始数的步数，则 *q 继续往前走一步，而 *b 从新走。如果 *q 所在当前步数不等于 *b 的从头开始数的步数，则存在环。这种方法可以找到环所在节点。

方法二：设置两个指针 *q 和*b都指向单链表的头结点。其中 *q 的移动速度是 *b 的 2 倍，若在某个时候*q == *b，则存在环。一般偶数量节点的单循环链表跑两次后*q == *b。

本文参考：
【C 语言描述】《数据结构和算法》（小甲鱼） (opens new window)